Aprenda a ordenar e pesquisar listas - aplicável a microcontroladores
Quem
trabalha com microcontroladores sabe que muitas vezes é necessário
utilizar matrizes, tabelas, pequenos arquivos e as vezes também
pequenos banco de dados, tudo inserido em sua memória (no formato
lista).
E em alguns casos, é necessário ordenar para posterior pesquisa. Este
artigo descreverá alguns métodos de ordenação e pesquisa considerados
básicos, mas que poderão ser aplicados com
qualquer microcontrolador presente no mercado atualmente.
MÉTODOS DE ORDENAÇÃO
Quando trabalhamos com listas, existem ocasiões em que necessitamos ordena-las para facilitar as pesquisas. Podemos ordenar os valores de uma matriz (ou banco de dados) do mais baixo para o mais alto (ordem crescente) ou ainda mais alto para o mais baixo (ordem crescente). Sem esse tipo de ordenação toda e qualquer pesquisa em uma matriz seria muito difícil e demorada. Basicamente o que teria de se fazer é posicionar o “ponteiro” no topo da matriz e ir comparando cada um dos elementos da matriz com o valor procurado. Para uma matriz pequena, esse "método" não é assim algo tão complexo e talvez seja o mais utilizado. Mas para matrizes um pouco maior, esse método consome muito tempo de processamento, tempo este que muitas vezes o sistema não dispões. Nestes casos o melhor é ordenar a matriz para somente então começar as pesquisas. Você deve estar neste momento pensado: “Mas a ordenação também não consome um tempo de processamento?”. A resposta para este pensamento é SIM. Mas você deve considerar que este processamento será realizado apenas uma única vez, durante a inicialização do sistema e/ou quando “muitos novos” elementos forem acrescentados. E creia, o tempo de processamento realizado numa ordenação é muito menor que o tempo de duas pesquisas feitas em uma base de dados desordenada. Sendo assim, vale a pena “ordenar”!
Existem alguns métodos (algoritmos) muito utilizados para ordenar matrizes (listas e/ou matrizes). São eles: Bubble Sort (ordenação tipo bolha), Select Sort (ordenação por seleção), Shell Sort (ordenação por divisão e inserção) e Quick Sort (ordenação por divisão e conquista). A seguir descreverei os mesmos.
ORDENAÇÃO BUBBLE SORT
O algoritmo Bubble Sort consome tempo e processamento. Apesar de simples, não deve ser utilizado com matrizes ou listas muito extensas para evitar lentidão no processamento.
Seu funcionamento é muito simples. O Algoritmo faz um loop (laço) pelos valores da matriz comparando-os e movendo o maior para a posição anterior. Este método cria uma ordenação decrescente. Para criar uma ordenação crescente, o algoritmo deverá mover o maior valor para a posição posterior, após o elemento testado. Veja um exemplo abaixo.
Modelo Bubble Sort
a)ordem decrescente
|
Lembrando sempre que a dificuldade de ordenação está relacionada com a disposição dos elementos na matriz (lista) e também com o número de elementos presentes na mesma. O box abaixo mostra um exemplo de segmento de código, desenvolvido na Linguagem de Programação C, para o modelo Bubble Sort.
Exemplo de segmento de código para Bubble Sort|
//***************************************************************************
// Função bubble_sorte – Recebe uma matriz desordenada e a ordena com // algoritmo bubble sort // // Entradas – matriz a ser ordenada e tamanho da matriz a ordenar // Saídas - nenhuma //*************************************************************************** void bubble_sort(unsigned char matriz[], unsigned int tamanho){ unsigned int i, j; unsigned char temp; for (i=0; i < tamanho; i++) for(j=0;j < tamanho; j++) if (matriz[i] < matriz[j]){ temp=matriz[i]; matriz[i]=matriz[j]; matriz[j]=temp; } } |
ORDENAÇÃO SELECT SORT
O algoritmo Select Sort também consome processamento e tempo, e assim, também não é adequado em matrizes e listas muito grandes. Ele trabalha selecionando um elemento como o primeiro da lista, por exemplo. É realizada uma pesquisa na lista para encontrar o valor mínimo e este é então posicionado no lugar do elemento pesquisado. A pesquisa continua procurando o segundo elemento menor (maior que o mínimo e menor que o selecionado). Esta ordenação será crescente. Para obter uma ordenação decrescente, basta operar o algoritmo de maneira contrária. A figura abaixo mostra um exemplo hipotético para este modo de ordenação, no modo crescente, e o box mais abaixo trás um exemplo de segmento de código do modelo Select Sort desenvolvido na Linguagem C.
Modelo Select Sort
|
|
//***************************************************************************
// Função select_sorte – Recebe uma matriz desordenada e a ordena com // algoritmo select sort // // Entradas – matriz a ser ordenada // - tamanho da matriz a ordenar // Saídas - nenhuma //*************************************************************************** void select_sort(unsigned char matriz[], unsigned int tamanho){ unsigned char temp; unsigned int atual, j; for (atual=0; atual < tamanho; atual++) for (j = atual + 1; j < tamanho; j++) if (matriz[atual] > matriz[j]){ temp=matriz[atual]; matriz[atual]=matriz[j]; matriz[j]=temp; } } |
ORDENAÇÃO SHELL SORT
A ordenação Shell Sort compara os elementos de uma matriz que estão separados por uma distância específica chamada gap até que os elementos comparados com o gap corrente estejam em ordem. O gap é então é dividido por 2 e o processo continua, até que o gap seja igual a 1 e nenhuma divisão possa mais ser feita (com um valor inteiro como resultado). Ao final do processo, a matriz estará ordenada.
Este método se parece muito com o algoritmo tipo bolha (Buble Sort) somado ao tipo seleção (Select Sort), com a diferença de ser mais rápido e podermos escolher quais elementos da matriz serão ordenados. Assim, este algoritmo pode ser considerado um dos que consome menor processamento e também tempo de execução. A figura abaixo demonstra um exemplo do algoritmo. No box mais abaixo vocêr encontrará um exemplo de segmento de código para o modelo Shell Sort desenvolvido na Linguagem C.
Modelo Shell Sort
|
|
//***************************************************************************
// Função shell_sorte – Recebe uma matriz desordenada e a ordena com // algoritmo shell sort // // Entradas – matriz a ser ordenada e tamanho da matriz a ordenar // Saídas - nenhuma //*************************************************************************** void shell_sort(unsigned char matriz[], unsigned int tamanho){ unsigned int i, gap; unsigned char temp, ret; gap = tamanho / 2; do { do{ ret=0; for (i=0; i< tamanho – gap; i++) if (matriz[i] >matriz[i+gap]){ temp=array[i]; array[i]=array[i+gap]; array[i+gap]=temp; ret=1; } } while(ret); } while (gap = gap / 2); } |
ORDENAÇAO QUICK SORT
Este algoritmo seleciona o valor central da lista como um separador. A partir daí ele cria duas listas: a primeira com os valores menores que o separador e outra com os valores maiores ou iguais ao separador. A seguir a ordenação chama a si mesma recursivamente, sempre selecionando um novo separador nas listas, e criando novas listas menores até que estas tenham apenas um único elemento. O algoritmo então reposiciona os valores das novas listas na lista original. Ao final do algoritmo uma matriz (lista) estará ordenada. A figura abaixo mostra um exemplo deste algoritmo.
Modelo Quick Sort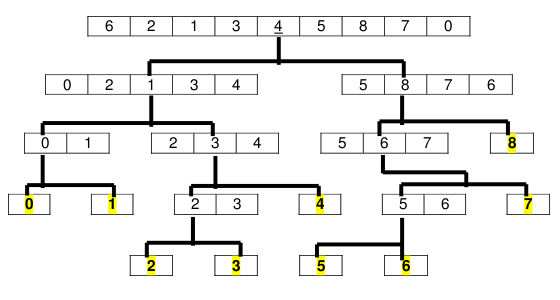
Note
que as novas “listas” são geradas levando em conta a posição
da lista anterior. Assim o programa saberá exatamente qual a posição
de cada valor. O leitor deve observar porém que neste método, o
consumo de memória é bem grande e isto, para alguns
microcontroladores, pode ser um fator limitante. O box 4
mostra um exemplo de segmento de código, desenvolvido na Linguagem
C, para a aplicação da Quick Sort.
|
//***************************************************************************
// Função quick_sorte – Recebe uma matriz desordenada e a ordena com // algoritmo quick sort // // Entradas – matriz a ser ordenada e índices – primeira e última posições // Saídas - nenhuma //*************************************************************************** void quick_sort(unsigned char matriz[], unsigned int primeiro, unsigned int ultimo){ unsigned char temp; unsigned int high, low, separador; low = primeiro; high = ultimo; separador = matriz[(primeiro + ultimo) / 2]; do { while(matriz[low] < separador) low++; while(matriz[high] > separador) high--; if (low <= high){ temp=matriz[low]; matriz[low++] = matriz[high]; matriz[high--] = temp; } } while (low <= high); if (primeiro < high) quick_sort(matriz, primeiro, high); if (low < ultimo) quick_sort(matriz, low, ultimo); } |
MÉTODOS DE PESQUISA
Como dito no início deste artigo “ordenar é preciso”. Se uma base de dados ou matriz está ordenada, nada melhor que aplicar os métodos corretos de pesquisa a mesma. E os algoritmos para pesquisa são muitos. Porém é possível destacar os dois principais e mais utilizados: Busca/Pesquisa Seqüencial e Busca/Pesquisa Binária.
BUSCA SEQUÊNCIAL
O algoritmo Busca Seqüencial executa a pesquisa de um elemento em uma matriz comparando-o aos elementos da matriz um após o outro até obter o resultado “verdadeiro” ou chegar ao fim da matriz. Este tipo de busca só é viável se a matriz (lista) for pequena (ou média) e/ou não estiver ordenada. Devido ao seu modo de operação, a mesma costuma consumir tempo. O box abaixo mostra um exemplo desenvolvido na Linguagem C (hipotético).
Segmento de código exemplo para Busca Seqüencial|
//***************************************************************************
// Função seek_seq – Realiza uma busca em uma matriz usando o algoritmo //busca seqüencial // // Esta função requer a criação da matriz em modo global, assim como // a definição do número máximo de elementos da mesma (ELEMENTOS_MATRIZ) // // Entradas – valor a ser procurado // Saídas - nenhuma //*************************************************************************** void seek_seq(unsigned int busca){ found = FALSE; i = 0; while ((i < ELEMENTOS_MATRIZ) && (!found)){ if (MATRIZ[I] == busca) found = TRUE; else i++; } if (i < ELEMENTOS_MATRIZ) printf(“Valor encontrado na matriz %d\n”,i); else printf(“Valor não encontrado”); } |
BUSCA BINÁRIA
A busca binária só deve ser executada em matrizes (listas) previamente ordenadas, seja no modo crescente ou decrescente. A pesquisa binária divide por dois a lista analisada e compara o valor. Se o valor central for maior que o objeto da pesquisa, o algoritmo divide novamente a lista em dois, desta vez considerando apenas a parte central e o topo da lista. Se o valor central for menor, a nova divisão será feita entre a parte central e o final da lista. Agora o algoritmo compara novamente o objeto da pesquisa com o valor apresentado e continua a divisão até obter o resultado positivo, ou até não ser mais possível realizar a divisão da matriz. Se isto ocorrer, é porque o valor não foi encontrado e o algoritmo devolve este resultado. Note que esta pesquisa é muito rápida e é a mais adequada para uso com matrizes (listas) muito grandes. O box abaixo mostra um segmento de código que pode ser utilizado como exemplo pelo leitor, para o algoritmo de Busca Binária.
Segmento de código exemplo para Busca Binária|
//***************************************************************************
// Função seek_bin – Realiza uma busca em uma matriz utilizando o algoritmo // busca binária // // Esta função requer a criação da matriz em modo global, assim como // a definição do número máximo de elementos da mesma (ELEMENTOS_MATRIZ) // // Entradas – valor a ser procurado // Saídas - nenhuma //*************************************************************************** void seek_bin(unsigned int valor){ found = 0; high = tamanho_da_lista; low = 0; middle = (high + low) / 2; while ((!found) && (high >= low)){ if (valor == MATRIZ[middle]) found = 1; else if (value < MATRIZ[middle]) high = middle –1; else low = middle + 1; mid = (high + low) /2; } } |
Obs: todos os exemplos passados foram preparados na Linguagem “C” e podem ser facilmente adaptados para outras linguagens de programação como BASIC, PASCAL e mesmo ASM, apenas baseando-se nos conceitos envolvidos. Um outro detalhe importante é que o segmento exemplo para Quick Sort utiliza a recursividade (uma função pode chamar a sí mesma, “n” vezes), muito comum para os programadores “C”. Porém este recurso não é permitido em alguns compiladores C para microcontroladores. Antes de utilizar o segmento demonstrado, certifique-se que seu compilador aceita “recursividade”.
CONCLUSÃO
Apesar de alguns compiladores oferecerem em suas bibliotecas poderosos recursos para ordenação e pesquisa em listas e outros, acredito que conhecer os métodos utilizados para tal seja importante para a formação do bom profissional. Assim quando você se deparar com um compilador que não possui “tais recursos”, poderá criá-los a partir do que foi explicado neste artigo, gerando assim suas próprias bibliotecas. Bons estudos com muitas ordenações e buscas! Até a próxima!